Introduction to Pytorch—Learning Tensors

Learning of Tensors

Tensors are a special data structure, very similar to arrays and matrices. In PyTorch, we use tensors to encode the input and output of the model, as well as the parameters of the model.

Tensors are similar to NumPy’s ndarrays, except that tensors can run on GPUs or other hardware accelerators. In fact, tensors and NumPy arrays can often share the same underlying memory, eliminating the need to copy data (see Bridging with NumPy). Tensors are also optimized for automatic differentiation (we will see more about this later in the Autograd section). If you are familiar with ndarrays, you will be familiar with the Tensor API.

import torch
import numpy as np

Initializing a Tensor Initializing a tensor

Directly from data Initialized directly from data

Tensors can be created directly from data. Data types are automatically inferred.

data = [[1, 2],[3, 4]]
x_data = torch.tensor(data)

From a NumPy array Initialized from a NumPy array

Tensors can be created from NumPy arrays (and vice versa — see Bridging with NumPy).

np_array = np.array(data)
x_np = torch.from_numpy(np_array)

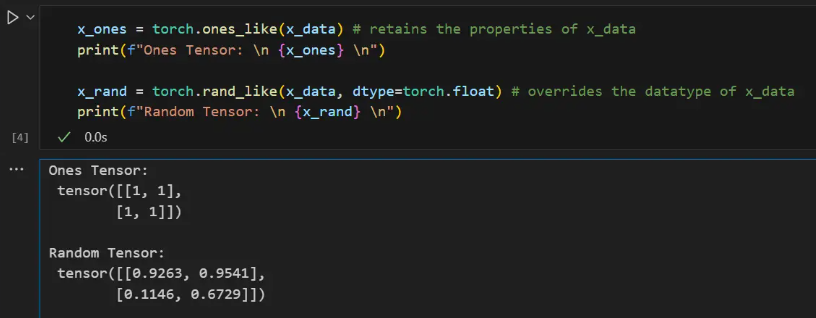
From another tensor Initialized from another tensor

The new tensor retains the properties (shape, data type) of the parameter tensor unless overridden explicitly.

x_ones = torch.ones_like(x_data) # retains the properties of x_data
print(f"Ones Tensor: \n {x_ones} \n")
​
x_rand = torch.rand_like(x_data, dtype=torch.float) # overrides the datatype of x_data
print(f"Random Tensor: \n {x_rand} \n")

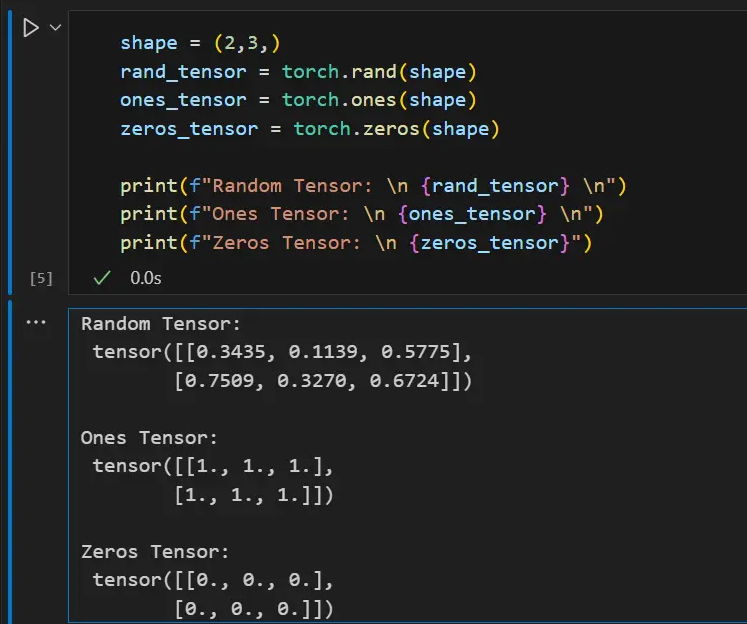
With random or constant values ​​With random or constant values

shapeis a tuple of tensor dimensions. In the function below, it determines the dimensionality of the output tensor.

shape = (2,3,)
rand_tensor = torch.rand(shape)
ones_tensor = torch.ones(shape)
zeros_tensor = torch.zeros(shape)
​
print(f"Random Tensor: \n {rand_tensor} \n")
print(f"Ones Tensor: \n {ones_tensor} \n")
print(f"Zeros Tensor: \n {zeros_tensor}")

Attributes of a Tensor

Tensor properties describe their shape, data type, and the device on which they are stored.

tensor = torch.rand(3,4)
​
print(f"Shape of tensor: {tensor.shape}")
print(f"Datatype of tensor: {tensor.dtype}")
print(f"Device tensor is stored on: {tensor.device}")

Standard numpy-like indexing and slicing Standard numpy-like indexing and slicing

tensor = torch.ones(4, 4)
print(f"First row: {tensor[0]}")
print(f"First column: {tensor[:, 0]}")
print(f"Last column: {tensor[..., -1]}")
tensor[:,1] = 0
print(tensor)

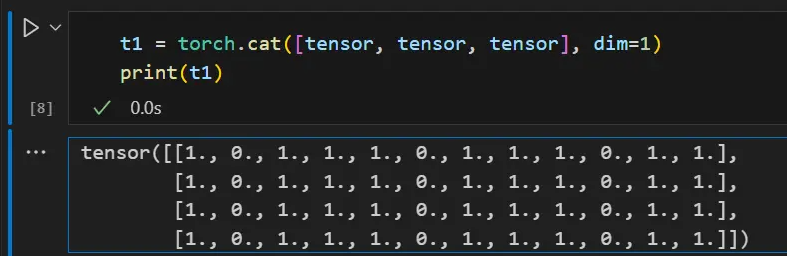
Joining tensors connecting tensors

Concatenating Tensors You can use torch.catto concatenate a sequence of tensors along a given dimension. See also torch.stack, another torch.catslightly different tensor concatenation operator than .

t1 = torch.cat([tensor, tensor, tensor], dim=1)
print(t1)

Arithmetic operations Arithmetic operations

# This computes the matrix multiplication between two tensors. y1, y2, y3 will have the same value
# ``tensor.T`` returns the transpose of a tensor
y1 = tensor @ tensor.T
y2 = tensor.matmul(tensor.T)
​
y3 = torch.rand_like(y1)
torch.matmul(tensor, tensor.T, out=y3)
​
​
# This computes the element-wise product. z1, z2, z3 will have the same value
z1 = tensor * tensor
z2 = tensor.mul(tensor)
​
z3 = torch.rand_like(tensor)
torch.mul(tensor, tensor, out=z3)

This code mainly demonstrates how to perform matrix multiplication and element-level multiplication in PyTorch.

0. Matrix multiplication:y1 = tensor @ tensor.Ty2 = tensor.matmul(tensor.T)Both lines of code and are doing matrix multiplication. Both @operators and matmulfunctions can be used for matrix multiplication. tensor.TReturns the transpose of tensor.y3 = torch.rand_like(y1)y1A new tensor with the same shape and random numbers as elements is created .torch.matmul(tensor, tensor.T, out=y3)This line of code is also doing a matrix multiplication, but the result is written directly y3instead of creating a new tensor.
1. Element-wise multiplication:z1 = tensor * tensorz2 = tensor.mul(tensor)Both lines of code and are doing element-wise multiplication. Both *operators and mulfunctions can be used for element-wise multiplication.z3 = torch.rand_like(tensor)tensorA new tensor with the same shape and random numbers as elements is created .torch.mul(tensor, tensor, out=z3)This line of code is also performing element-wise multiplication, but the result is written directly z3instead of creating a new tensor.

What are matrix multiplication and element-wise multiplication?

Matrix multiplication and element-wise multiplication are two different mathematical operations.

0. Matrix multiplication : Also known as dot product, it is a binary operation that multiplies two matrices to produce a third matrix. Suppose we have two matrices A and B. The shape of A is (m, n) and the shape of B is (n, p). Then we can perform matrix multiplication to get a new matrix C whose shape is (m, p). ). Each element in C is obtained by multiplying the corresponding elements of the row vector of A and the column vector of B and then summing them.
1. Element-wise multiplication : also known as Hadamard product, is a binary operation that multiplies two matrices to produce a third matrix. Suppose we have two matrices A and B with the same shape, then we can perform element-wise multiplication to get a new matrix C with the same shape as A and B. Each element in C is obtained by multiplying the corresponding elements in A and B.

In Python’s NumPy and PyTorch libraries, you can use the @or matmulfunction for matrix multiplication and the *or mulfunction for element-wise multiplication.

Single-element tensors

single element tensor

If you have a single-element tensor, for example by aggregating all the values ​​of the tensor into a single value, you can item()convert it to a Python numeric value using .

agg = tensor.sum()
agg_item = agg.item()
print(agg_item, type(agg_item))

In-place operations

local operation

An operation that stores the result in an operand is called an in-place operation. They _are represented by the suffix. For example: x.copy_(y), x.t_(), will change x.

print(f"{tensor} \n")
tensor.add_(5)
print(tensor)

NOTE Note In-place operations save some memory, but can cause problems when calculating derivatives because the history is lost immediately. Therefore, their use is discouraged.

Bridge with NumPy

Tensors on CPU and NumPy arrays can share their underlying memory locations, and changing one will change the other.

Tensor to NumPy array

t = torch.ones(5)
print(f"t: {t}")
n = t.numpy()
print(f"n: {n}")

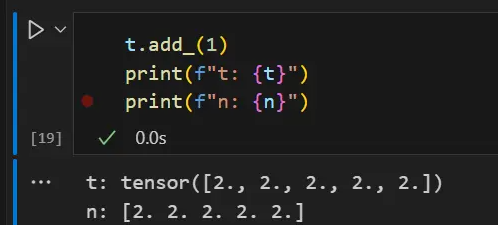
Changes to the tensor are reflected in the NumPy array.

t.add_(1)
print(f"t: {t}")
print(f"n: {n}")

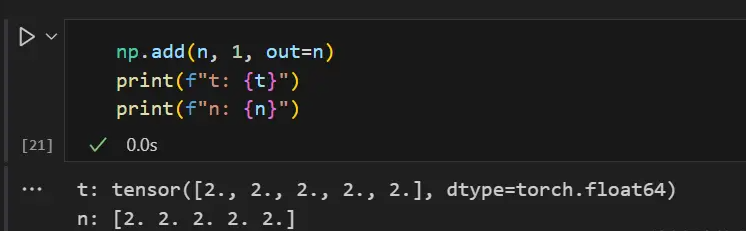
NumPy array to tensor

n = np.ones(5)
t = torch.from_numpy(n)

Changes in NumPy arrays are reflected in tensors.

np.add(n, 1, out=n)
print(f"t: {t}")
print(f"n: {n}")